Questões de Matemática - Fatec

Em determinada semana do mês de maio, o departamento financeiro de uma empresa fez, na ordem apresentada, as seguintes retiradas:

• 1/6 do saldo disponível para pagar uma fatura a vencer naquela semana;
• 20% do restante para a compra de materiais de escrtório e
• o valor de R$ 3.200.00 para pagamento da manutenção de um equipamento eletrônico.

Sabendo-se que, naquela semana, não ocorreram outras movimentações financeiras e que as retiradas realizadas resultaram em um saldo positivo de R$ 12.000,00, então o saldo disponível, antes das retiradas, era

Argamassa é uma mistura de cimento, cal, areia e água a qual serve para o assentamento de tijolos, revestimento de superfícies e execução de juntas.

Uma mistura de cimento, cal e areia será preparada de modo que para cada parte de cimento haja duas partes de cal e nove partes de areia.

Usando como unidade de medida uma lata de 18 litros, a quantidade de areia para preparar 300 latas dessa mistura será, em metros cúbicos.

A figura representa a vista superior de uma piscina e suas dimensões internas.

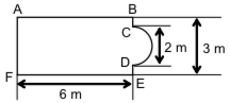
Na figura, temos o seguinte:

• ABEF é um retângulo de dimensões 3 m por 6 m, e
• o arco CD é uma semicircunferência com diâmetro 2 m.

Considerando que a profundidade da piscina é constante e igual a 1,2 m, a capacidade da piscina é, em litros,

Uma academia possui duas salas contíguas e retangulares: uma para ginástica e a outra para ioga, conforme mostra a figura.

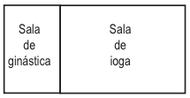
Para adequar o atendimento aos usuários, a academia realizou uma reforma em que a sala de ginástica foi transformada em um quadrado, aumentando o lado menor em 2 metros. Dessa maneira, a sala de ioga foi reduzida de 30 m² para 18 m².

A área da antiga sala de ginástica, em metros quadrados, era

Um recipiente, no qual será acondicionado um líquido de densidade 0,9 g/cm³, tem o formato geométrico de um prisma reto quadrangular.

Sabe-se que

• a base do prisma é um quadrado de lado 10 cm;
• a massa do líquido a ser acondicionado no recipiente é 1,8 kg e
• o líquido ocupa 80% da capacidade do recipiente.

Nessas condições, a altura do recipiente, em centímetros, é

Em um supermercado, a probabilidade de que um produto da marca A e um produto da marca B estejam a dez dias, ou mais, do vencimento do prazo de validade é de 95% e 98%, respectivamente. Um consumidor escolhe, aletoriamente, dois produtos, um produto da marca A e outro da marca B.

Admitindo eventos independentes, a probabilidade de que ambos os produtos escolhidos estejam a menos de dez dias do vencimento do prazo de validade é

Considere a matriz . A soma dos elementos da matriz M² é

Considere o texto a seguir para responder às questões de números 33 e 34.

As “áreas de coberturas” a serem atendidas por um serviço de telefonia móvel são divididas em células, que são iluminadas por estações-radiobase localizadas no centro das células.

As células em uma mesma área de cobertura possuem diferentes frequências, a fim de que uma célula não interfira na outra. Porém, é possível reutilizar a frequência de uma célula em outra célula relativamente distante, desde que a segunda não interfira na primeira.

Cluster é o nome dado ao conjunto de células vizinhas, o qual utiliza todo o espectro disponível. Uma configuração muito utilizada está exemplificada na Figura 1, que representa um modelo matemático simplificado da cobertura de rádio para cada estação-base.

O formato haxagonal das células é o mais prático, pois permite maior abrangência de cobertura, sem lacunas e sem sobreposições.

A figura 2 ilustra o conceito de reutilização de frequência por cluster, em que as células com mesmo número utilizam a mesma frequência.

www.teleco.com.br/tutorial/tutorialatalaia/pagina_2.asp e www.teleco.com.br/tutorialsmsloc/pagina_3.asp Acesso em: 05.10.2012. Adaptado)

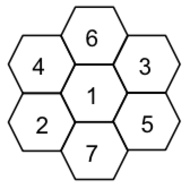Figura 1: Cluster de sete células

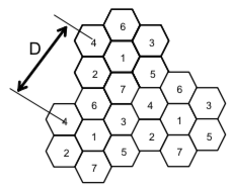Figura 2: Reuso de frequência

Na figura 2, os hexágonos são congruentes, regulares, têm lado de medida R e cobrem uma superfície plana. Para determinar a distância D, distância mínima entre o centro de duas células que permitem o uso da mesma frequência, pode-se traçar um triângulo cujos vértices são os centros de células convenientemente escolhidas, conforme a figura 3.

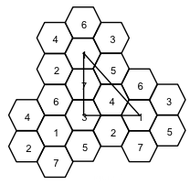Figura 3

Assim sendo, o valor D, expresso em função de R, é igual a

(Texto para responder às questões de números 33 e 34)

Um modelo da perda (L) de propagação de sinais entre a antena transmissora e a receptora em espaço livre de obstáculos é, em decíbel (dB), expressa por

em que f é a frequência de transmissão em mega-hertz (MHz) e d é a distância entre as anternas de transmissão e recepção em quilômetros (km).

Considerando que um sinal de radiofrequência de 600 MHz é enviado de uma estação-base para uma antena receptora que está a 20 km de distância, em espaço livre, então o valor da perda de propagação desse sinal é, em dB, aproximadamente,

Na figura, a reta representa parte do gráfico de uma função do 1.° grau.

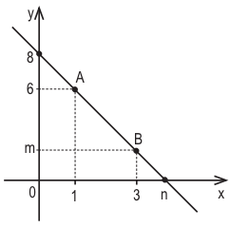
Sabendo-se que A(1; 6), B(3; m) e que a reta corta os eixos x e y, respectivamente nos pontos (n; 0) e (0; 8), conclui-se corretamente que o valor de m + n é