Uma das primeiras estimativas do raio da Terra é atribuída a Eratóstenes, estudioso grego que viveu, aproximdamente, entre 275 a.C. e 195 a.C. Sabendo que em Assuã, cidade localizada no sul do Egito, ao meio dia do solstício de verão, um bastão vertical não apresentava sombra, Eratóstenes decidiu investigar o que ocorreria, nas mesmas condições, em Alexandria, cidade no norte do Egito. O estudioso observou que, em Alexandria, ao meio dia do solstício de verão, um bastão vertical apresentava sombra e determinou o ângulo entre as direções do bastão e de incidência dos raios de sol. O valor do raio da Terra, obtido a partir de
e da distância entre Alexandria e Assuã foi de, aproximadamente, 7500km.
O mês em que foram realizadas as observações e o valor aproximado de são
Note e adote
Distância estimada por Eratóstenes entre Assuã e Alexandria é aproximadamente 900 km.
Clique aqui e faça uma pergunta na sessão de comentários desta questão.
Vinte times de futebol disputam a Série A do Campeonato Brasileiro, sendo seis deles paulistas.
Cada time joga duas vezes contra cada um dos seus adversários. A porcentagem de jogos nos quais os dois oponentes são paulistas é
Clique aqui e faça uma pergunta na sessão de comentários desta questão.
São dados, no plano cartesiano, o ponto P de coordenadas (3,6) e a circunferência C de equação (x–1)2 +(y–2)2 =1. Uma reta t passa por P e é tangente a C em um ponto Q. Então a distância de P a Q é
Clique aqui e faça uma pergunta na sessão de comentários desta questão.
Uma jovem estudante quis demonstrar para sua mãe o que é uma reação química. Para tanto, preparou, em cinco copos, as seguintes soluções:
| Copo | Solução |
|---|---|
| 1 | vinagre |
| 2 | sal de cozinha + água |
| 3 | fermento químico (NaHCO3) + água |
| 4 | açúcar + água |
| 5 | suco de limão |
Em seguida, começou a fazer misturas aleatórias de amostras das soluções contidas nos copos, juntando duas amostras diferentes a cada vez. Qual é a probabilidade de que ocorra uma reação química ao misturar amostras dos conteúdos de dois dos cinco copos?
Clique aqui e faça uma pergunta na sessão de comentários desta questão.
Os vértices de um tetraedro regular são também vértices de um cubo de aresta 2. A área de uma face desse tetraedro é
Clique aqui e faça uma pergunta na sessão de comentários desta questão.
As propriedades aritméticas e as relativas à noção de ordem desempenham um importante papel no estudo dos números reais. Nesse contexto, qual das afirmações abaixo é correta?
Clique aqui e faça uma pergunta na sessão de comentários desta questão.
Sejam e
números reais com
e
. Se o sistema de equações, dado em notação matricial,
,
for satisfeito, então é igual a
Clique aqui e faça uma pergunta na sessão de comentários desta questão.
Quando se divide o Produto Interno Bruto (PIB) de um país pela sua população, obtém-se a renda per capita desse país. Suponha que a população de um país cresça à taxa constante de 2% ao ano. Para que sua renda per capita dobre em 20 anos, o PIB deve crescer anualmente à taxa constante de, aproximadamente,
Dado:
Clique aqui e faça uma pergunta na sessão de comentários desta questão.
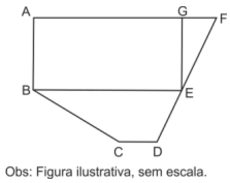
O mapa de uma região utiliza a escala de 1: 200 000. A porção desse mapa, contendo uma Área de Preservação Permanente (APP), está representada na figura, na qual e
são segmentos de reta, o ponto G está no segmento AF, o ponto E está no segmento
, ABEG é um retângulo e BCDE é um trapézio.
Se AF=15, AG=12, AB=6, CD=3 e DF= indicam valores em centímetros no mapa real, então a área da APP é
Clique aqui e faça uma pergunta na sessão de comentários desta questão.
Seja f uma função a valores reais, com domínio , tal que
, para todo
.
O conjunto que pode ser o domínio D é
Clique aqui e faça uma pergunta na sessão de comentários desta questão.
Página 1 de 4