Questões de Matemática - Unicamp

A figura abaixo exibe, em porcentagem, a previsão da oferta de energia no Brasil em 2030, segundo o Plano Nacional de Energia.

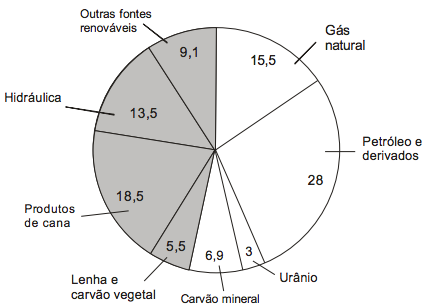
Segundo o plano, em 2030, a oferta total de energia do país irá atingir 557 milhões de tep (toneladas equivalentes de petróleo). Nesse caso, podemos prever que a parcela oriunda de fontes renováveis, indicada em cinza na figura, equivalerá a

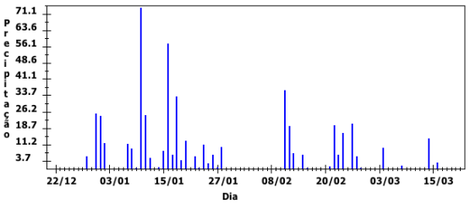
A figura abaixo mostra a precipitação pluviométrica em milímetros por dia (mm/dia) durante o último verão em Campinas. Se a precipitação ultrapassar 30 mm/dia, há um determinado risco de alagamentos na região. De acordo com o gráfico, quantos dias Campinas teve este risco de alagamento?

(Fonte: http://www.agritempo.gov.br/agroclima/plotpesq.Acessado em 10/10/2012.)

Um investidor dispõe de R$ 200,00 por mês para adquirir o maior número possível de ações de certa empresa. No primeiro mês, o preço de cada ação era R$ 9,00. No segundo mês houve uma desvalorização e esse preço caiu para R$ 7,00. No terceiro mês, com o preço unitário das ações a R$ 8,00, o investidor resolveu vender o total de ações que possuía. Sabendo que só é permitida a negociação de um número inteiro de ações, podemos concluir que com a compra e venda de ações o investidor teve

Para repor o teor de sódio no corpo humano, o indivíduo deve ingerir aproximadamente 500 mg de sódio por dia. Considere que determinado refrigerante de 350 ml contém 35 mg de sódio. Ingerindo-se 1.500 ml desse refrigerante em um dia, qual é a porcentagem de sódio consumida em relação às necessidades diárias?

Um automóvel foi anunciado com um financiamento “taxa-zero” por R$ 24.000,00 (vinte e quatro mil reais), que poderiam ser pagos em doze parcelas iguais e sem entrada. Para efetivar a compra parcelada, no entanto, o consumidor precisaria pagar R$ 720,00 (setecentos e vinte reais) para cobrir despesas do cadastro. Dessa forma, em relação ao valor anunciado, o comprador pagará um acréscimo

O perímetro de um triângulo retângulo é igual a 6,0 m e as medidas dos lados estão em progressão aritmética (PA). A área desse triângulo é igual a

Um caixa eletrônico de certo banco dispõe apenas de cédulas de 20 e 50 reais. No caso de um saque de 400 reais, a probabilidade do número de cédulas entregues ser ímpar é igual a

Ao decolar, um avião deixa o solo com um ângulo constante de 15°. A 3,8 km da cabeceira da pista existe um morro íngreme. A figura abaixo ilustra a decolagem, fora de escala.

Podemos concluir que o avião ultrapassa o morro a uma altura, a partir da sua base, de

Considere as funções f e g, cujos gráficos estão representados na figura abaixo.

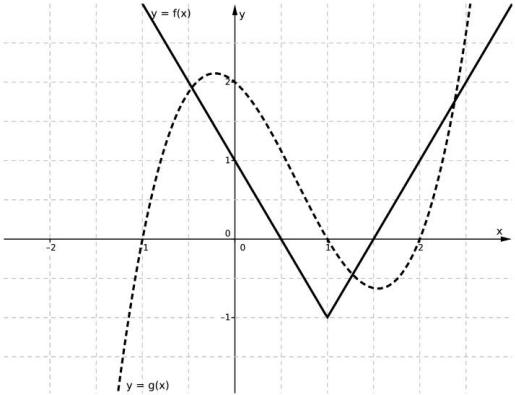
O valor de f(g(1))) - g(f(1)) é igual a

Uma barra cilíndrica é aquecida a uma temperatura de 740°C. Em seguida, é exposta a uma corrente de ar a 40°C. Sabe-se que a temperatura no centro do cilindro varia de acordo com a função

sento t o tempo em minutos, T₀ a temperatura inicial e T_AR a temperatura do ar. Com essa função, concluímos que o tempo requerido para que a temperatura no centro atinja 140°C é dado pela seguinte expressão, com o log na base 10: