Questões de Matemática - Enem

O diretor de uma escola convidou os 280 alunos de terceiro ano a participarem de uma brincadeira. Suponha que existem 5 objetos e 6 personagens numa casa de 9 cômodos; um dos personagens esconde um dos objetos em um dos cômodos da casa. O objetivo da brincandeira é adivinhar qual objeto foi escondido por qual personagem e em qual cômodo da casa o objeto foi escondido.

Todos os alunos decidiram participar. A cada vez um aluno é sorteado e dá a sua resposta. As respostas devem ser sempre distintas das anteriores, e um mesmo aluno não pode ser sorteado mais de uma vez. Se a resposta do aluno estiver correta, ele é declarado vencedor e a brincadeira é encerrada.

O diretor sabe que algum aluno acertará a resposta porque há

Um biólogo mediu a altura de cinco árvores distintas e representou-as em uma mesma malha quadriculada, utilizando escalas diferentes, conforme indicações na figura a seguir.

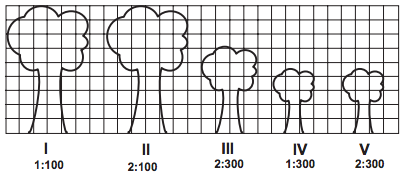
Qual é a árvore que apresenta a maior altura real?

Em um jogo há duas urnas com 10 bolas de mesmo tamanho em cada urna. A tabela a seguir indica as quantidades de bolas de cada cor em cada urna.

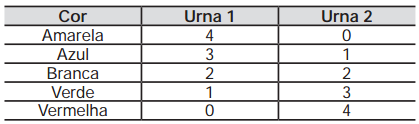
Uma jogada consiste em:

1. o jogador apresenta um palpite sobre a cor da bola que será retirada por ele da urna 2;

2. ele retira, aleatoriamente, uma bola da urna 1 e a coloca na urna 2, misturando-a com as que lá estão;

3. em seguida ele retira, também aleatoriamente, uma bola da urna 2;

4. se a cor da última bola retirada for a mesma do palpite inicial, ele ganha o jogo.

Qual cor deve ser escolhida pelo jogador para que ele tenha a maior probabilidade de ganhar?

Os hidrômetros são marcadores de consumo de água em residências e estabelecimentos comerciais. Existem vários modelos de mostradores de hidrômetros, sendo que alguns deles possuem uma combinação de um mostrador e dois relógios de ponteiro. O número formado pelos quatro primeiros algarismos do mostrador fornece o consumo em m³, e os dois últimos algarismos representam, respectivamente, as centenas e dezenas de litros de água consumidos. Um dos relógios de ponteiros indica a quantidade em litros, e o outro em décimos de litros, conforme ilustrados na figura a seguir.

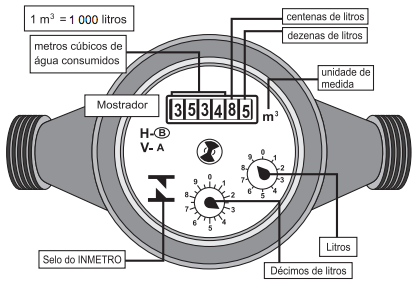Disponível em: www.aguasdearacoiaba.com.br (adaptado).

Considerando as informações indicadas na figura, o consumo total de água registrado nesse hidrômetro, em litros, é igual a

O dono de uma farmácia resolveu colocar à vista do público o gráfico mostrado a seguir, que apresenta a evolução do total de vendas (em Reais) de certo medicamento ao longo do ano de 2011.

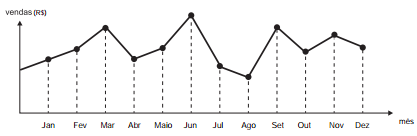
De acordo com o gráfico, os meses em que ocorreram, respectivamente, a maior e a menor venda absolutas em 2011 foram

Maria quer inovar em sua loja de embalagens e decidiu vender caixas com diferentes formatos. Nas imagens apresentadas estão as planificações dessas caixas.

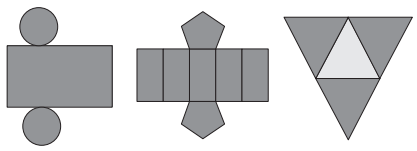
Quais serão os sólidos geométricos que Maria obterá a partir dessas planificações?

Jogar baralho é uma atividade que estimula o raciocínio. Um jogo tradicional é a Paciência, que utiliza 52 cartas. Inicialmente são formadas sete colunas com as cartas. A primeira coluna tem uma carta, a segunda tem duas cartas, a terceira tem três cartas, a quarta tem quatro cartas, e assim sucessivamente até a sétima coluna, a qual tem sete cartas, e o que sobra forma o monte, que são as cartas não utilizadas nas colunas.

A quantidade de cartas que forma o monte é

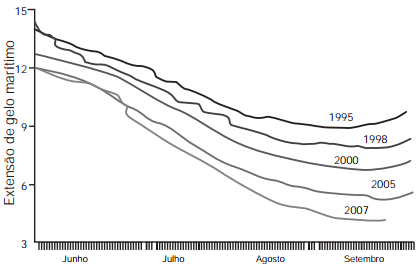
O gráfico mostra a variação da extensão média de gelo marítimo, em milhões de quilômetros quadrados, comparando dados dos anos 1995, 1998, 2000, 2005 e 2007. Os dados correspondem aos meses de junho a setembro. O Ártico começa a recobrar o gelo quando termina o verão, em meados de setembro. O gelo do mar atua como o sistema de resfriamento da Terra, refletindo quase toda a luz solar de volta ao espaço. Águas de oceanos escuros, por sua vez, absorvem a luz solar e reforçam o aqucimento do Ártico, ocasionando derretimento crescente do gelo.

Disponível em: http://sustentabilidade.allianz.com.br. Acesso em: fev. 2012 (adaptado).

Com base no gráfico e nas informações do texto, é possível inferir que houve maior aquecimento global em

Uma pesquisa realizada por estudantes da Faculdade de Estatística mostra, em horas por dia, como os jovens entre 12 e 18 anos gastam seu tempo, tanto durante a semana (de segunda-feira a sexta-feira), como no fim de semana (sábado e domingo). A seguinte tabela ilustra os resultados da pesquisa.

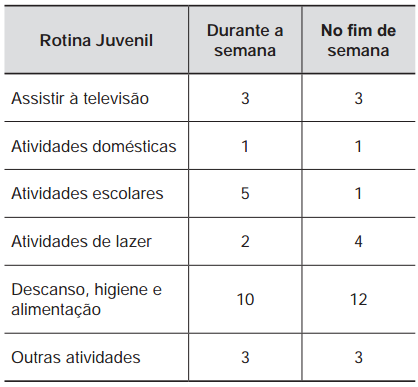
De acordo com esta pesquisa, quantas horas de seu tempo gasta um jovem entre 12 e 18 anos, na semana inteira (de segunda-feira a domingo), nas atividades escolares?

Certo vendedor tem seu salário mensal calculado da sguinte maneira: ele ganha um valor fixo de R$ 750,00, mais uma comissão de R$ 3,00 para cada produto vendido. Caso ele venda mais de 100 produtos, sua comissão passa a ser de R$ 9,00 para cada produto vendido, a partir do 101º produto vendido.

Com essas informações, o gráfico que melhor representa a relação entre salário e o número de produtos vendidos é