Racha Cuca

Teoria dos Conjuntos

Na matemática consideramos o conjunto como um ente primitivo, ou seja, aceitamos o mesmo sem definição.

Podemos, no entando intuitivamente, dar exemples de conjuntos como: conjuntos de objetos, de letras, de números, de pessoas, e assim sucessivamente.

Por estes motivos damos o nome de conjunto a qualquer agrupamento, associação, junção de objetos. Esses agrupamentos terão algum caráter comum. Os objetos serão chamados de elementos do conjunto.

Representação de Conjuntos

Um conjunto pode ser representado por uma letra maiúscula, em geral do alfabeto latino, e os elementos são colocados entre chaves e separados por vírgulas.

Exemplos

O conjunto das vogais: V = {a, e, i, o, u}.
Podemos também dar uma característica dos elementos do conjunto: V = {x | x é uma vogal}.
E ainda podemos representar o conjunto por uma figura plana fechada que chamamos de de diagrama de EULER-VENN.

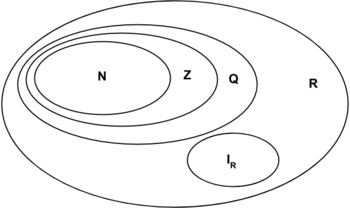Diagrama dos números reaisNeste caso não há necessidade de separar os elementos com vírgula.Neste caso não há necessidade de separar os elementos com vírgula.

Para trabalharmos com conjuntos necessitamos de uma simbologia adequada que em grande parte foi elaborada pelo italiano Giuseppe Peano (1858-1932), um dos grandes estudiosos da teoria dos conjuntos, deixando uma valiosa colaboração a respeito da mesma.

Símbolos

  • \in : pertence
  • \notin : não pertence
  • \subset : está contido
  • \not \subset : não está contido
  • \supset : contém
  • \not \supset : não contem
  • \exists : existe
  • \not \exists : não existe
  • \emptyset : conjunto vazio
  • \forall : para todo ou qualquer que seja
  • \mid : tal que
  • \Rightarrow : implica que
  • \Leftrightarrow : se, e somente se

Símbolos das Operações

  • A \cap B : A intersecção B
  • A \cup B : A união B
  • a \: . \: b : diferença de A com B
  • a < b : a menor que b
  • a \leq b : a menor ou igual a b
  • a > b : a maior que b
  • a \geq b : a maior ou igual a b
  • a \wedge b : a e b
  • a \vee b : a ou b

Relação de Pertinência

Para indicar que um elemento "x" pertence ao conjunto "A", escreve-se: x \in A

Para exprimir que esse mesmo elemento não pertence ao conjunto "A", escreve-se: x \notin A

Exemplo

A = {1, 3, 9, 15}

  • 3 pertence a A: 3 \in A
  • 5 não pertence a A: 5 \notin A

Relação de Inclusão

  • Para indicar que um conjunto "B" está contido num conjunto "A", escreve-se: B \subset A .
  • Para exprimir que um conjunto "B" está não contido num conjunto "A", escreve-se: B \not \subset A .

Entretanto, podemos representar a ideia anterior de outra forma:

  • Para indicar que um conjunto "A" está contém um conjunto "B", escreve-se: B \supset A .
  • Para indicar que um conjunto "A" está não contém um conjunto "B", escreve-se: B \not \supset A .

Conjunto Unitário

É um conjunto que possui um só elemento.

Exemplos

  • P = {x | x simboliza o Papa atual}
  • S = {7}

Conjunto Vazio

É um conjunto que não possui elementos. Símbolo: \emptyset ou { }.

Conjunto Infinito

É um conjunto que possui infinitos elementos.

Exemplos

  • A = {x | x > 1}
  • B = {-2, -1, 0, 1, 2, ...}

Conjunto Finito

É um conjunto que possui um número determinado de elementos.

Exemplos

  • C = {-4, 0, 3, 5}
  • D = {x | x é consoante}

União de Conjuntos

Dados dois conjuntos "A" e "B", chama-se união desses conjuntos, e escreve-se A \cup B , ao conjunto constituído pelos elementos de "A" ou de "B".

A \cup B = \{x | x \in A \: ou \: x \in B\}

Exemplos

  • A = {1, 2, 3, 4} e B = {4, 5, 6}. A \cup B = \{1, 2, 3, 4, 5, 6\}
  • A = {3, 4, 5} e B = {7, 8}. A \cup B = \{3, 4, 5, 7, 8\}

Intersecção de Conjuntos

Dados dois conjuntos "A" e "B", chama-se intersecção desses conjuntos, e escreve-se A \cap B , ao conjunto constituído pelos elementos comuns de "A" e de "B".

Exemplos

  • A = {1, 4, 6, 8, 10} e B = {2, 3, 5, 8, 10}. A \cap B = \{8, 10\}
  • A = {2, 4, 6, 8, 9} e B = {4, 6}. A \cap B = \{4, 6\}

Subconjuntos

Para calcular o número de subconjuntos de um conjunto dado podemos utilizar a relação 2^{n} , onde n representa o número de elementos do conjunto dado.

Exemplo

O conjunto A = {a, b, c} possui 8 subconjuntos: {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, {a, b, c}, \emptyset .

Ao conjunto formado pelos subconjuntos {{a}, {b}, {c}, {a, b}, {a, c}, {b, c}, {a, b, c}, \emptyset }, damos o nome de conjunto das partes de A.

Complementar

O complemento (ou coplementar) de um conjunto "A", em relação a um conjunto "B", assim se define: C_A^B = B - A

Exemplo

  • A = {2, 4, 5} e B = {1, 2, 3, 4, 5}. C_A^B = B - A = \{1, 3\}

Observação

O complementar de um conjunto A, por exemplo, pode ser representado por \overline{A} .

Bibliografia
  • Domingos, Oslei. Apostila de Matemática Pré-Vestibular - Projeto Eureka. Governo do Paraná.

Conteúdos relacionados

5

Racha Cuca+